| 4C. Uitwerkingen. | ||||
|
Opgave 1. a. Aselect gecontroleerd b. Onafhankelijk: ja/nee (vit.C of niet?); Afhankelijk: ja/nee (symptomen verkoudheid of niet?) c. Eenzijdig; alternatieve hypothese is "minder verkoudheid". d. Reduceert Vitamine C de kans op verkoudheid? e. Nulhyp.: Vit.C heeft geen effect; er is geen verschil; proportie testgroep - proportie controlegroep = 0; Alternatieve Hyp.: Vit.C heeft positief effect; proportie testgroep - proportie controlegroep < 0 f. Twee proporties vergelijken g. Prop.test: 17/139=0,1223 ; Prop.contr: 31/140=0,2214; Verschil: -0,0991 Bootstrap levert 95%-BTI dat loopt van -0,185 tot -0,006; de 0 ligt er niet in. 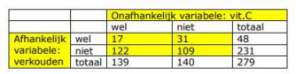 h. Het steekproefresultaat is significant, bij een significantieniveau van 2,5%; de Vitamine C reduceert de kans op verkoudheid; er is 2,5% kans dat deze uitspraak onjuist is. i. Oorzakelijk verband, want de onderzoeksopzet werkt met een test- en controlegroep die via een toevalsmechanisme zijn toegekend; bovendien is de opzet dubbel-blind. j. Je kunt niet naar alle Europeanen generaliseren, omdat de test- en controlegroep bestaat uit een lokaal en fysiek beperkt groepje mensen k. Om dat wel te kunnen doen moeten de deelnemers aan de test- en controlegroep met een toevalsmechanisme uit de populatie van alle Europeanen gekozen worden! | ||||
|
Opgave 2. a. Randomized: toekenning van personen aan test- of controlegroep gebeurt door een toevalsmechanisme. Double-blind: de proefpersonen weten niet of ze wel of niet een echte vitaminepil kregen; de dokters die op verkoudheid controleerden weten het ook niet. Placebo-controlled: een onderdeel van double-blind, nl. iedereen krijgt een pil, maar bij een placebo-pil lijkt die op een vitaminepil, maar zit er geen werkzame stof in. b. Nulhyp.: Vit.C heeft geen effect; er is geen verschil; proportie testgroep - proportie controlegroep = 0; Alternatieve Hyp.: Vit.C heeft positief effect; proportie testgroep - proportie controlegroep < 0. c. Bootstrap levert 95%-BTI dat loopt van -0,01 tot +0,01; de 0 ligt er wel in. De nulhypothese is dus nog aannemelijk. Het waargenomen verschil kan nog een gevolg van toeval zijn. 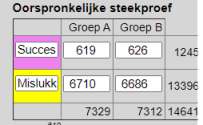 | ||||
Opgave 3.
Alt.hypothes: dit verschil is positief (ptest - pcontr>) > 0. App: twee proporties vergelijken; bootstrap gebruiken.
b. Laten we veronderstellen dat de twee groepen aselect gecontroleerd zijn. Dan zou het een oorzakelijk verband zijn. Maar het is zeker niet dubbelblind. Want je weet wel degelijk in welke groep je zit! En dan nóg: er is niet gekeken of er wel werkelijk gestopt is met roken; alleen naar wat iemand op dat moment zegt. | ||||
|
Opgave 4. a. Aselect gecontroleerd b. Onafhankelijk: ja/nee (kreeg je een gaap-zaadje of niet?) Afhankelijk: ja/nee (ging je zelf gapen of niet?) c. Eenzijdig; alternatieve hypothese is "meer gapen". d. Is gapen besmettelijk? e. Nulhyp.: Gapen heeft geen effect; er is geen verschil; proportie testgroep - proportie controlegroep = 0; Alternatieve Hyp.: Gapen heeft positief effect; proportie testgroep - proportie controlegroep > 0 f. Twee proporties vergelijken g. Prop.test: 24/68=0,3529 ; Prop.contr: 4/32=0,1250; Verschil: 0,2279 Bootstrap levert 95%-BTI dat loopt van 0,06 tot 0,38; de 0 ligt er niet in. 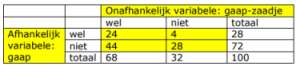 h. Het steekproefresultaat is significant, bij een significantieniveau van 2,5%; gapen is besmettelijk; er is 2,5% kans dat deze uitspraak onjuist is. i. Je kunt spreken over een oorzakelijk verband omdat de indeling in test- en controlegroep met een toevalsmechanisme gebeurde. j. Maar deze conclusie beperkt zich tot de populatie van de deelnemers aan deze test; de populatie is veel te beperkt: een plaatselijke vlooienmarkt. k. Dan had je de deelnemers aan het gaap-onderzoek niet op een plaatselijke vlooienmarkt moeten uitkiezen, maar via een toevalsmechanisme uit alle Europeanen! | ||||
|
Opgave 5. a. Aselect gecontroleerd b. Onafhankelijk: ja/nee (kreeg je goede pleister) Afhankelijk: ja/nee (kreeg een placebo) c. Eenzijdig; alternatieve hypothese is "meer gestopt". d. Werkt de pleisterk? e. Nulhyp.: Pleister heeft geen effect; er is geen verschil; (proportie stoppen in testgroep) - (proportie stoppen in controlegroep) = 0; Alternatieve Hyp.: Pleister heeft positief effect; (proportie stoppen in testgroep) - (proportie stoppen in controlegroep) > 0 f. Kruistabel invullen in "Twee proporties vergelijken"; rechts bovenaan staat: 1,9 keer zoveel kans om te stoppen.  g. Bootstrap levert 95%-BTI van het relatieve risico, dat loopt van 1,38 tot 2,74. h. Nulhyp.: Pleister heeft geen effect; (proportie stoppen in testgroep) / (proportie stoppen in controlegroep) = 1; Alternatieve Hyp.: Pleister heeft positief effect; (proportie stoppen in testgroep) / (proportie stoppen in controlegroep) > 1 i. Het steekproefresultaat is significant, bij een significantieniveau van 2,5%; want de waarde 1 ligt niet in het 95%-BTI bij eenzijdig gebruik; conclusie: de pleister helpt. j. Nee, natuurlijk niet; ik kan met deze beslissing alleen maar zeggen dat het (veel of weinig) helpt; maar ik kan net het 95%-BTI wél aangeven hoe goed het ongeveer helpt. k. De pleisters zorgen er immers voor dat je tussen 1,4 en 2,7 keer zo'n grote kans hebt om te stoppen met roken, vergeleken met rokers die de pleisters niet gebruiken. m. Omvang steekproef 4 keer zo klein: de variabiliteit van de proporties wordt 2 keer zo groot volgens de wortel-n-wet. Het BTI wordt dus 2 keer zo breed. Het zou dus best kunnen zijn dat de 1 nu wél in het blauwe gebied van het BTI komt te liggen! Laten we eens proberen met de simulatie. Alles 4 keer zo klein. Het relatieve risico is nog steeds 1,9.  Bootstrap levert 95%-BTI van het relatieve risico, dat loopt van 1,00 tot 4,33. Je ziet dat de 1 nu net op de rand van het blauwe gebied ligt. Ik zou dus concluderen dat het nog net acceptabel is dat dit steekproefresultaat het gevolg van toeval is. Ik durf met deze kleine steekproef niet te concluderen dat de pleisters helpen. En de schatting van het relatieve risico in de hele populatie is ook een stuk onnauwkeuriger geworden. Met grotere steekproeven heb je dus meer kans dat je kunt beslissen dat de pleisters helpen en is je schatting van het effect van de pleisters nauwkeuriger. Het is wel zo dat 4 keer zo veel werk in je onderzoek maar twee keer zoveel nauwkeurigheid oplevert! | ||||
Opgave 6.
- Kruistabel invullen in "Twee proporties vergelijken"; rechts bovenaan staat: verschil proporties M en N is -0,194. - Tweezijdig: neem dus 95%-BTI als je een significantiedrempel van 5% aanhoudt. - Bootstrap levert 95%-BTI van het verschil, dat loopt van -0,349 tot -0,031. - Het verschil NUL ligt in het rode gebied, en is dus niet meer acceptabel als parameter voor de populatie; het steekproefresultaat is significant, bij een significantieniveau van 5%; conclusie: er IS verschil tussen jongens en meisjes in profielkeuze Maatschappij of Natuur. N.B.: ik zeg er hier niet bij dat de meisjes vaker Maatschappij kiezen, want dat was niet mijn vooraf geformuleerde alternatieve hypothese! - Als ik kijk naar het 95%-BTI van het relatieve risico, dan vind ik: 0,37 tot 0,93; dat betekent dat ik wél met 95% zekerheid kan zeggen: de aandeel jongens in de hele populatie bij Maatschappij is tussen 37 en 93% van het aandeel jongens bij Natuur. | ||||
|
Opgave 7. - Eenzijdig; ik veronderstel dat het gemiddelde cijfer Natuur hoger is in de populatie - Neem dus 90%-BTI als je een significantiedrempel van 5% aanhoudt. - Bootstrap levert 90%-BTI van het verschil, dat loopt van -0,87 tot -0,32. - Het verschil NUL ligt in het rode gebied, en is dus niet meer acceptabel als parameter voor de populatie; het steekproefresultaat is significant, bij een significantieniveau van 5%; conclusie: het gemiddelde wiskundecijfer in profielkeuze Maatschappij is lager dan dat bij Natuur. - Ik kan met 90% zekerheid zeggen: in de hele populatie is het gemiddelde wiskundecijfer bij Maatschappij tussen de 0,32 en 0,87 punt lager dan bij Natuur. | ||||
|
Opgave 8. - Gebruik "Kentallen"; Gemidd = 8,43 en SD = 2,24 - Gem + SD = 10,67; rechts schuiven: 13%; niet helemaal de vereiste 1% uit de vuistregels. - Gem - SD = 6,19; links schuiven : 17,4%; ook niet helemaal. Dus een iets scheve bijne normal verdeling. - Tweezijdig. Significantiedrempel 5%. Dus 95%-B-BTI nemen. - De schatting loopt van 8,05 tot 8,81. - Conclusie: de Amsterdamse leerlingen wijkt significant af van het landelijke gemiddelde 8,0. - Veronderstelling: de groep leerlingen van de gymleraar is een aselecte steekproef uit de Amsterdamse jongens van 14 jaar. - Bij een 4 keer zo kleine steekproef hoort een √4 = 2 keer zo breed B-BTI; dan zou het resultaat van de steekproef wel eens niet meer significant kunnen zijn. | ||||
Opgave 9.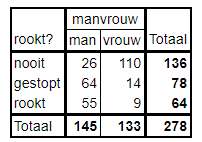 - Tweezijdig; want je er staat niks over een idee dat vrouwen meer of minder zouden roken; - dus 95%-B-BTI - "nooit gerookt" (succes) tegenover "gestopt+rookt nog" (mislukking): BTI rel.ris. tussen 0,14 en 0,30; p(man)/p(vr)=0,14 betekent: p(vr)/p(man)= 7; p(man)/p(vr)=0,30 betekent: p(vr)/p(man)= 3; dus vrouwen hebben tussen 3 en 7 keer zo vaak nooit gerookt als mannen. - "nooit gerookt" (succes) tegenover "rookt nog" (mislukking): BTI rel.ris. tussen 0,24 en 0,46; dus vrouwen roken nog tussen 2 en 4 keer zo weinig als mannen. - Veronderstelling: de groep mannen en vrouwen is een aselecte steekproef uit (bijv.) Nederland. - Bij een 10 keer zo grote steekproef hoort een √10 = 3,2 keer zo smal B-BTI; je schatting wordt dan ruim 3 keer zo nauwkeurig. |

copyright